パスカル的三角形 〜Pascal-Like Triangles Made From A Game〜
関西学院高等部数理科学部が研究しているPascal-Like Trianglesを元に作成したアプリです.
数理科学部のメンバーによって発見され証明されている, ロシアンルーレット(Russian Roulette)の公式を用いて算出した値が出力されます.
この公式から算出される値は, 実際にロシアンルーレットゲームをする際に有用となるものであり, 同様のゲームをする際の
確率論的な見通しを算出できます.
一般の方にも有用です.
定義は以下の通りです.
(以下, TeX形式で記述)
(definition)
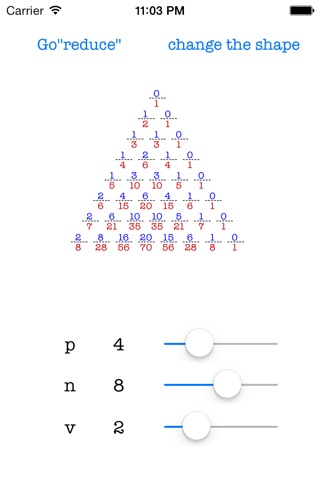
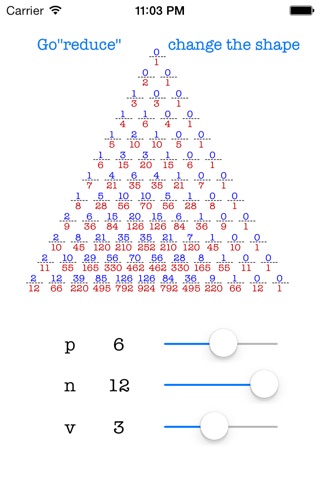
p人の参加者で, n個のシリンダ, m個の実弾の拳銃を用いたとき, v番目のプレイヤが負ける確率をf(p,n,m,v)とすると, 以下の式を満たす.
$ F(p, n, m, v) =sum_{z=0}^{t-1} {R (n, m, v + pz)}= sum_{z=0}^{t-1} {frac{{}_{n-v-pz} C _{m-1}}{{}_n C _m}}$ ,
where $ t = lfloor frac{n - m + p - v + 1}{p} rfloor$
(This Applications condition)
2 leq p leq 12, 2 leq n leq 12,1 leq v leq p,and m leq n.
p,n,vのスライダを動かすと, それらの値に対応する三角形が出力されます.
拡張機能として, 以下の機能を実装しています.
Go "reduce"(もしくはGo "no reduce")をタップ := 既約分数と可約分数の切り替え.
change the shape := pascal-like triangles(分数表示)とpascal-like triangles(分子のみの表示)の切り替え.
(References)
T. Hashiba, Y. Nakagawa, T. Yamauchi, H. Matsui, S. Hashiba, D. Minematsu, M. Sakaguchi, and R. Miyadera, "Pascal-like Triangles and Sierpinski-like Gaskets," Visual Mathematics: Art and Science Electronic Journal of ISIS-Symmetry [online], 9(1), 2007.
"Pascal-like Triangles Made from a Game"
http://demonstrations.wolfram.com/PascalLikeTrianglesMadeFromAGame/
(Members)
Programming, Upper Planning and etc by Masanori Fukui(ER Computing).
Icon making by Ryo Hanafusa(Kwansei Gakuin University).
(Special Thanks)
Dr.Ryohei Miyadera(Kwansei Gakuin Senior High School), and Kwansei Gakuin Senior High School Mathematical Sciences Club All Members.